Here the aim is to compare the performance of the three methods under
varying amounts of noise. Each time, the noise in the same image was
increased and then the three methods were tried upon it
using the same initial boundary placement.
The three methods were allowed to run roughly for the same
number of iterations
or when a method stops as the change between successive iterations
falls below a certain predetermined level.

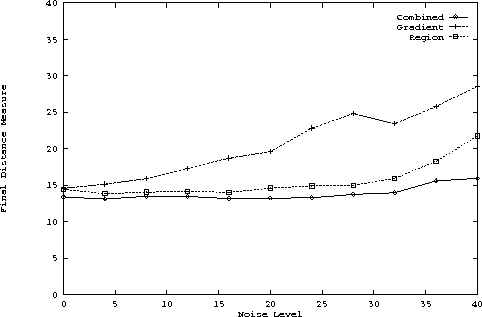
Figure 2 shows a comparison of the three methods. Here, the X-axis corresponds to the noise level given by the standard deviation of the noise used. The Y-axis gives a measure of the distance between the approximated contour and the true one. (This is a scaled version of the square of the distance between the contours.) Here in this and all the following plots, 'Gradient' represents the gradient based method, 'Region' corresponds to the boundary found based only on the region classified image, and 'Combined' refers to the proposed integration method. As we may expect, all the three methods perform worse as we increase the amount of noise. However, as we can see the combined method is the least sensitive to noise. Also, it performs much better compared to the traditional gradient based method. Since the gradient based method relies upon the first derivative, it is more susceptible to noise than the region based method, which uses homogeneity within the image. On the other hand, the combined method seems to give uniformly better results.
In
Fig 8
we
show the result for a particular value of the noise
given by .
Here we can see the comparison between the different
methods visually.
The initial boundary is considerably displaced and disfigured
as compared to the actual boundary. At some places, it is
inside the central region and at some other places it is
moved in the background. Neither region based segmentation nor
gradient based boundary finding works well for this noisy image.
However, as we can easily see, the combined method produces the best
result.
The next part of the experiment is to see how fast the
methods converge.
Figure 3 shows the situation when the image used has a
noise level given by . Clearly, the combined
method performs better than the other two, especially compared to the
gradient-based boundary finding. However, as the next plot, Figure 4
shows, when we have much lesser noise, given by
,
there is very little difference between the three methods.
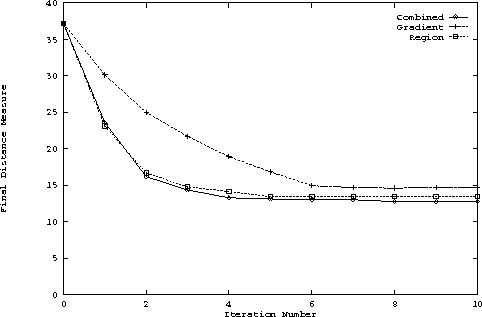
If we compare the above two plots it can clearly be observed that the proposed method using the combined approach is very insensitive to noise, as its performance does not vary considerably even after doubling the amount of noise. On the other hand, the normal gradient based method is extremely noise sensitive, and the performance deteriorates rapidly as we increase the amount of noise.
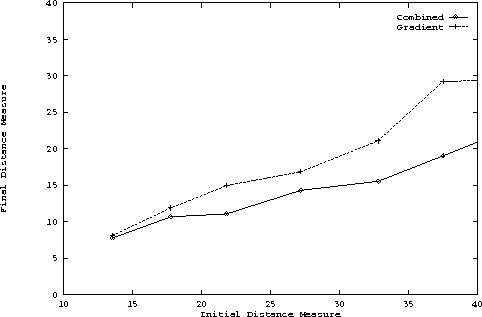
All the above was done using the same starting position as we may see
in Fig 8. The next plot, Figure 5 shows the situation under different starting
positions. Since different contours representing different starting
positions can have the same distance from the true contour, we had to
use average distance. Thus each point in the plot corresponds to
an average of the performance of the methods when presented with
almost similar initial distances but different contours.
Almost always, the integrated effort is better than pure gradient
based boundary finding.