In the previous experiment, we were handling situations where both
the methods that were combined
in our proposed method
produced reasonable results at least
under low noise situations. As we increased the amount of noise,
the gradient based method started making more and more errors.
However, there might be situations where one or both the methods
might produce unrealistic results. To investigate such a situation,
we devised an experiment with a synthetic occlusion.
If we look at
Fig 9
(top, left) we can see that for a part of
the image the intensity is lowered to a level slightly above the background.
However, as it touches the background there is a further fall
in the intensity level. On top of this as in the previous case,
we smooth the boundaries and add noise to it.
A similar thing may happen in a medical X-ray image where
an object may be just behind part of another object which is
of interest. Now if we do region
based segmentation under the assumption that there are two regions then all that part of the
central region beyond the artificial occlusion boundary will be
classified with the background as can be seen in the figure.
Thus as far as the based segmentation
is concerned, it sees an occlusion. Now, if we base the boundary finding
on this region classified image, it would tend to pull its boundary to the occlusion
boundary. For those parts where there is no occlusion, it
would still work. But for those parts where there is occlusion it
would make gross mistakes resulting in huge overall error.
But the gradient based method doesn't see much of a difference as
it searches for a local gradient maxima, which is still there.
Since the initialization is closer to the actual boundary than the occlusion
boundary, the gradient based method ignores the occlusion boundary.
Under these circumstances, if we try to get the performance plot in the
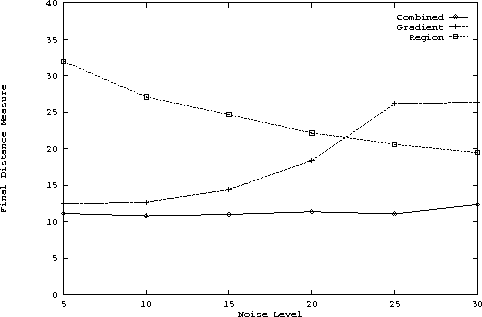
same way as we did in the previous case, we get the plot in Figure 6
where the axes and the legends have the same meaning as before.

Once again we can observe that the combined method performs much better compared to all the other methods. As expected, under low noise situations, the gradient based method and the proposed integrated method are close. But as we increase the amount of noise the deterioration is very rapid for the gradient method. But the combined method, shows very little response to increased amounts of noise. This confirms the results that we had in the last experiment. But a very interesting thing happens with the region based method. The plot seems to suggest an unreasonable thing: as the amount of noise increases, the performance improves. This apparent anomaly can be explained as follows. Since there is an occlusion, under low noise, the boundary comes close to the actual one where there is no occlusion, but where the occlusion is present, it pulls the boundary to the occlusion boundary. This results in large amounts of error. As we increase the amount of noise it becomes more probable for the optimization process to get trapped in a local minima resulting in smaller amount of movement. Thus it makes more mistakes at those positions where there is no occlusion, but at positions where there is occlusion it makes less error compared to the low noise case. This is so as the true boundary is closer to the initial boundary than the occlusion boundary. However, as we keep increasing the noise level, the characteristics flatten out and would again start rising for a further increase in noise. Figure 9 shows the occluded image and the performance of the different methods as described previously when applied on this image. It is easy to observe that the combined method performs the best.
As in the previous case, the next part of the experiment is concerned
with the speed of convergence. The setting is identical to the
last experiment except that we are now working on the occluded
image.
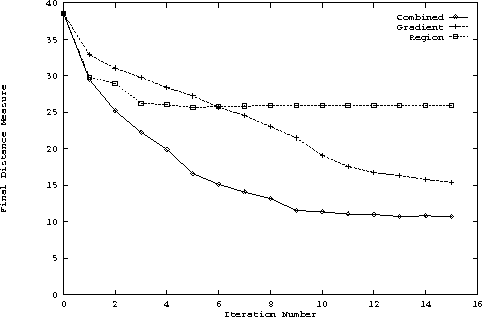
Once again, as we can see in Figure 7 the combined method performs much better. But gradually with larger and larger number of iterations, the gradient method comes closer to it because the region based method does not contribute much to the improvement process except for those regions where there is no occlusion. For the first few iterations, most of the change takes place in the region based method at those places where there is no occlusion and thus local information is available. But once this is done, it starts getting worse as the boundary starts getting closer and closer to the occlusion boundary.
Thus even if one of the methods fail partly, the integrated approach still seems to give reasonable results as it uses information from both the methods.